并查集

今天给朋友找资料时，无意中翻出了当年写的Kruskal算法的实现代码。说实话现在再看当年自己写的代码，已经看不懂了。其中在判断选边之后会不会形成闭环回路时，用到了并查集，因为当时是现用现学的，所以还是有些生疏，今天又拿出来翻了翻。说真的，这个结构以及算法是真的简洁实用。

普通并查集

并查集，说白了就是一个用数组来表示一个连通图，并且其内部元素构成一种树形结构。它可以用来判断元素之间的连通性，方式是通过判断两个元素是否属于同一个集合。那么如何判断？

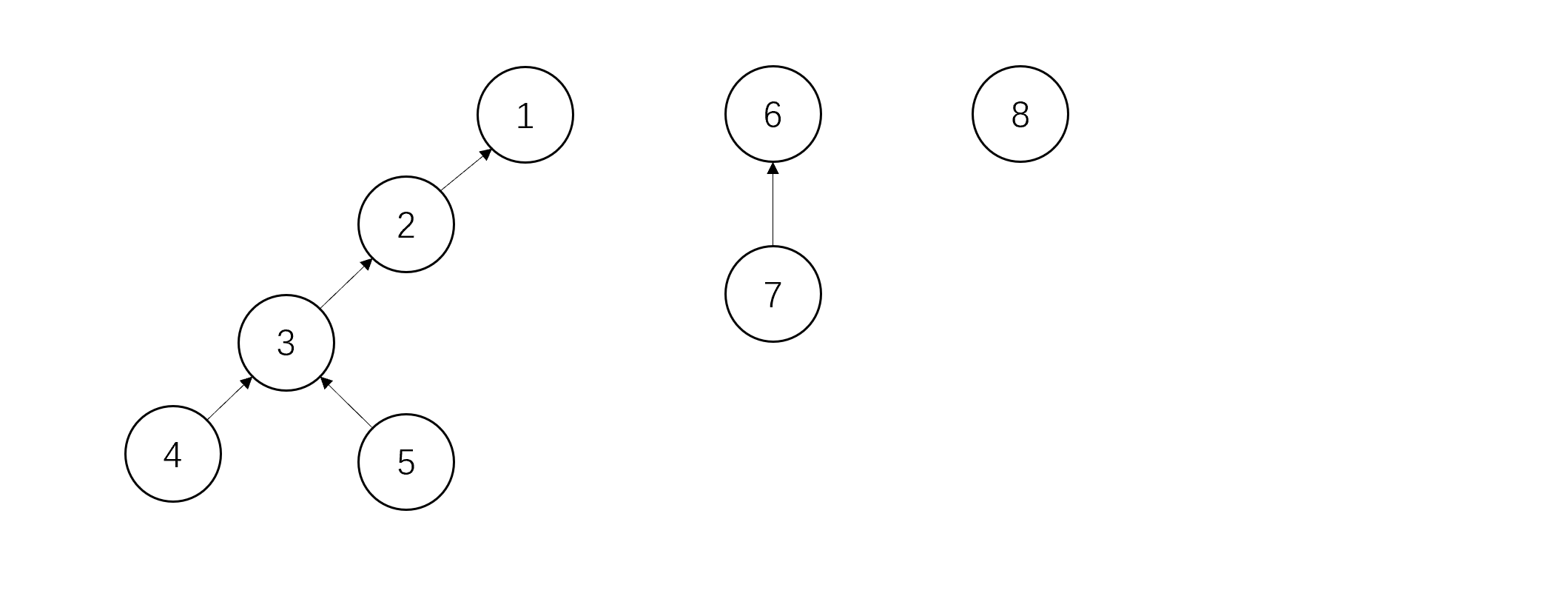
如图可见，有三个集合（3个树)，他们根分别是1，6和8。现在我要判断元素3和元素7是不是在一个集合内，我们只要分别的追溯出他们的根节点，判断他们的根节点是否一致。若一致，则处在一个集合内；若不一致，则不在一个集合内。很显然，对于元素3，其根节点为1；对于元素7，其根节点为6。那么3和7就不在一个集合内。

思想很简单，但最后终归要落实在代码上。为了方便操作，我们让并查集对应的数组满足一定的性质：数组下标i表示集合中的元素i，数组中第i个元素表示集合中元素i的父节点，根节点的父节点为它本身。例如：S[7]=6表示集合中的元素7的父节点为元素6；S[6]=6表示集合中的元素6的父节点为元素6自身，这表明6为根节点。

以上图中最左面的集合为例，在数组中它表示为：S[1]=1, S[2]=1, S[3]=2, S[4]=3, S[5]=3。

那么，对于查找根节点的操作，可以用下面的Find函数来实现：

SetType Find(SetType X)
{
	if (S[X] == X)
		return X;   //若是根节点，返回
	else
		return Find(S[X]); //若不是根节点，递归寻找
}

对于合并操作的代码：

void SetUnion(SetType X, SetType Y)
{
    SetType Root1 = Find(X), Root2 = Find(Y);
    if(Root1 == Root2) return;
    S[Root2] = Root1;
}

对于某一类问题，如果它并不需要连通图中每个节点的具体信息，只需要获得图中连通节点的数量或者需要用图的连通性去判断一些其他条件时，并查集相比其他图的表示方式是最佳的选择。

按秩优化

最简单的并查集很好实现。原理可能有些不容易懂，但代码很简洁。实在不行就背
但上述代码实现可能会造成一个问题，就是所有节点都集中在树的一侧：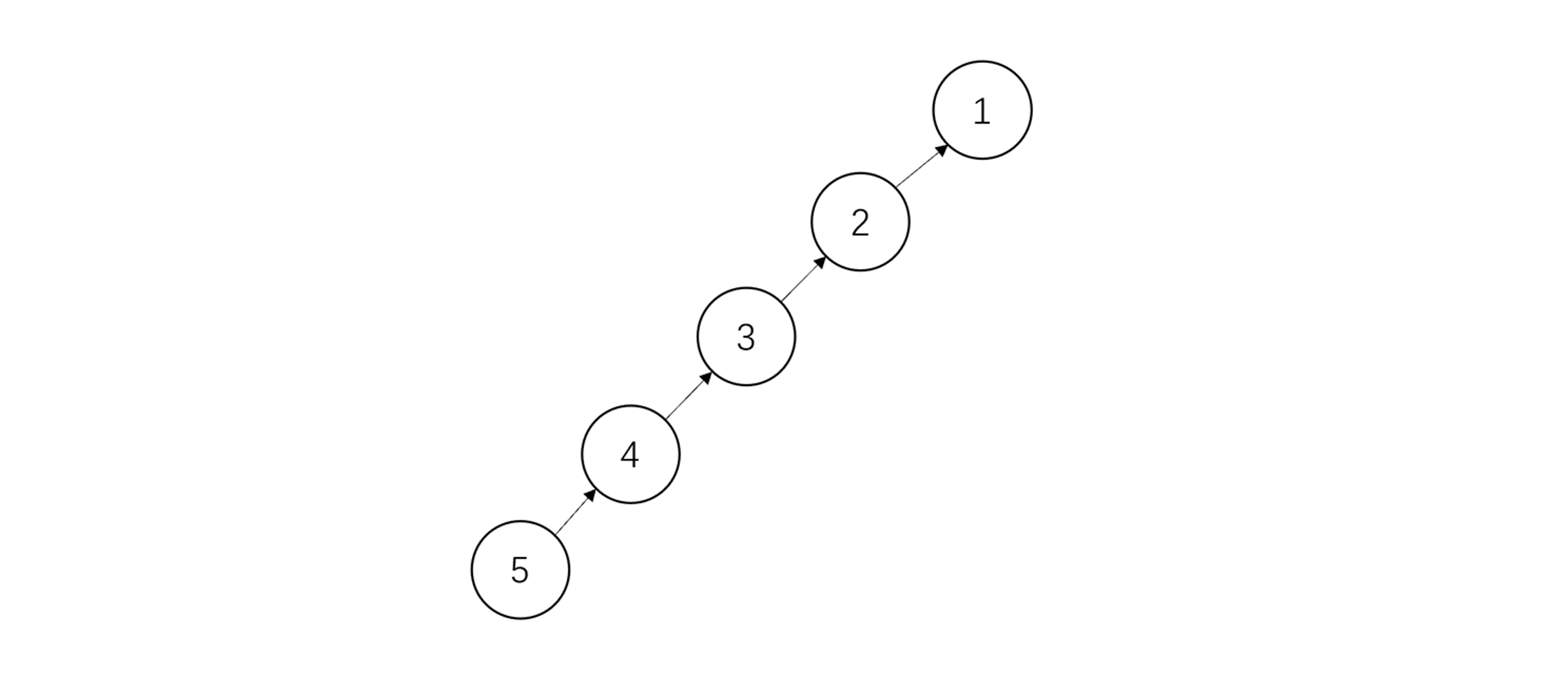

在上述的Find函数中，我们可以看出对于根节点的寻找是需要一个一个往回追溯的，树越高，节点越多，所耗费的时间越大。

这里探讨其中一种优化思路：按秩优化。

其思想也很简单，由于对于根节点的寻找是需要一个一个往回追溯的，那么自然树越小，所耗费的时间就越小。那么我们在合并两个集合的时候，尽量把小树往大树上合并。

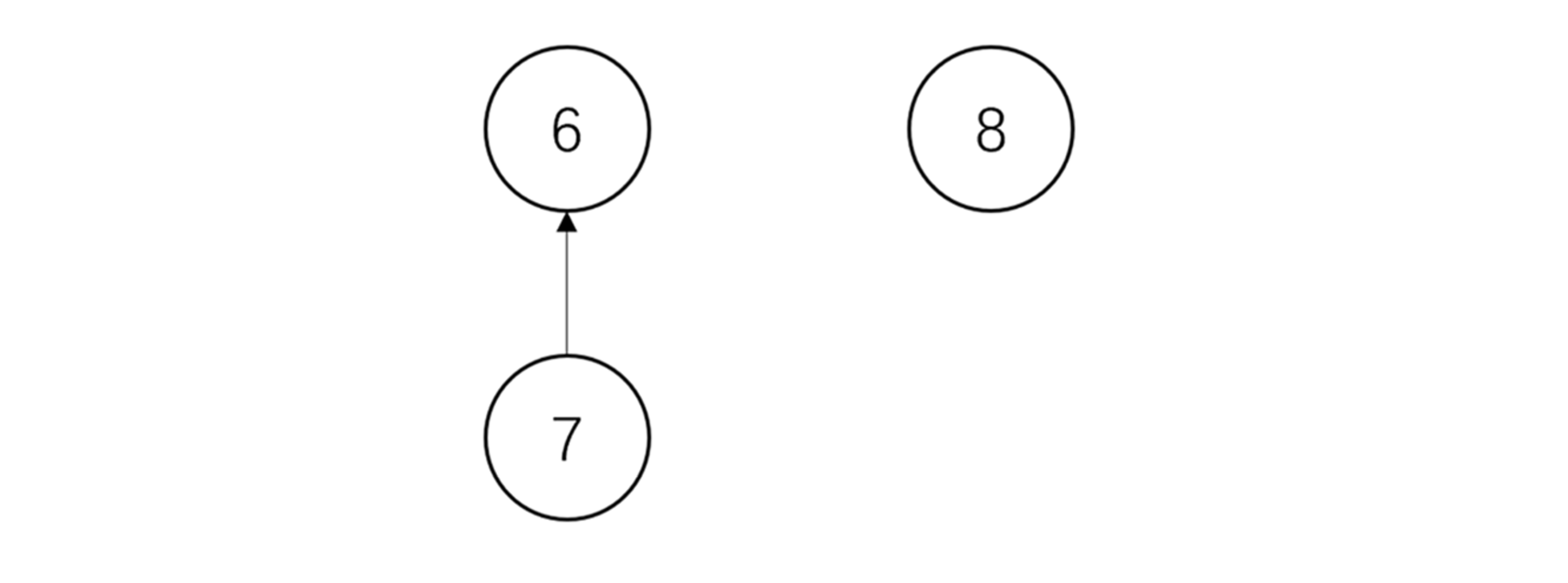
还是这两个集合，很明显，左树的规模大于右树，若我们将节点6接在节点8下，新树的高度相比左树还增加了1；若我们将节点8接在节点6下，新树的高度仍是左树的高度。此处可以证明，如果合并操作都是按大小进行的，那么任何节点的深度均不会超过$logN$。

形式一

由上述可见，此优化的核心是记录各个集合树的大小并作比较。在此，我们增加一个大小等同于并查集数组S的数组Rank来记录每个元素作为根节点时树的大小。

除按高度外，也可以将树的高度作为rank来进行合并。很明显，按高度合并是按大小合并的一种简易版，因为只有两个高度相等的树合并时秩才会增加，这样代码会更加简洁。与上述相似，只是将rank中的值改为树的高度。
此处给出的代码是按高度合并。不要问为什么不写按大小合并，因为那个写起来更麻烦

void SetUnion(SetType X, SetType Y)
{
    SetType Root1 = Find(X), Root2 = Find(Y);
    if(Root1 == Root2) return;
	if (Rank[Root2] > Rank[Root1])
		S[Root1] = Root2;
	else
	{
		if (Rank[Root1] == Rank[Root2]) //两个集合高度一致，随便挑一个将其接在另一个上
			Rank[Root1]++;
		S[Root2] = Root1;
	}
}

上面已经讲到，对于按高度合并，只有两个高度相等的树合并时秩才会增加，而且每次增加只会+1。所以在上述代码中，只有在Rank1等于Rank2时，我们才将秩+1。若是采用按大小合并，每次合并操作都需要更新根节点的Rank值，相较之下就麻烦了许多。

形式二

但上述这么写的弊端是需要额外申请一个数组的空间。在此提供一个简易的写法：对于根节点，其对应的数组元素中我们不再存储它本身，而是存储秩，即树的高度或大小。此处给出的代码仍是按高度合并：

void SetUnion(SetType X, SetType Y)
{
    SetType Root1 = Find(X), Root2 = Find(Y);
    if(Root1 == Root2) return;
	if (S[Root2] < S[Root1])
		S[Root1] = Root2;
	else
	{
		if (S[Root1] == S[Root2])
			S[Root1]--;
		S[Root2] = Root1;
	}
}

上述代码中的秩是以一个负值来表示的。其中需要注意的是，若采用此种方式，在初始化集合的时候，每个元素对应的值应该为-1，因为每个节点在初始化时都是一棵树，而这些树的高度均为1。在我的Kruskal算法中就采用的此种方式，但其实我当时根本不知道什么是按秩优化。

两种按秩优化方式的复杂度均为最坏情况下树的高度，即$O(log_2N)$。

路径压缩

对于上述一个串类型的树，我们还可以采用路径压缩的优化方式。其核心思想相比按秩优化稍有些复杂：在我们第一次追溯根节点的过程中，其实我们已经隐式地知晓了某个节点是否是根节点。那么我们是否可以在追溯的过程中，将树做一些改变，这样在下一次查找的过程中就可省下一些时间？

其核心步骤为：将操作节点接在其父节点的父节点上。

这样有些难以理解，咱们来举个例子。对于下面这样的并查集：

假设我们此次操作是查找元素4的根节点，那么我们第一次查找S[4]发现S[4]的值为3，说明4不是根节点，那么我们在递归节点3的同时，将4接在其父节点的父节点上，也就是节点2：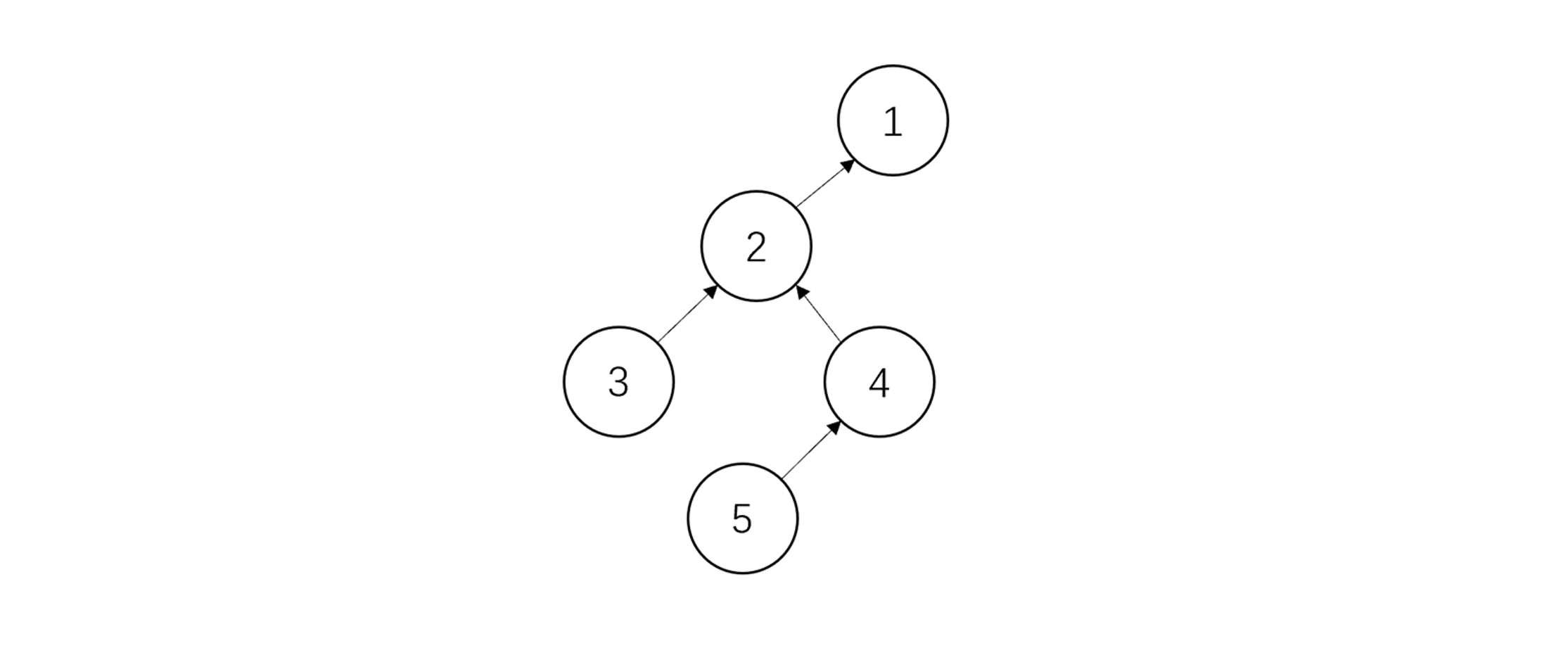

下一次递归时，我们操作的是节点3。同样，我们将其接在父节点的父节点上，也就是节点1：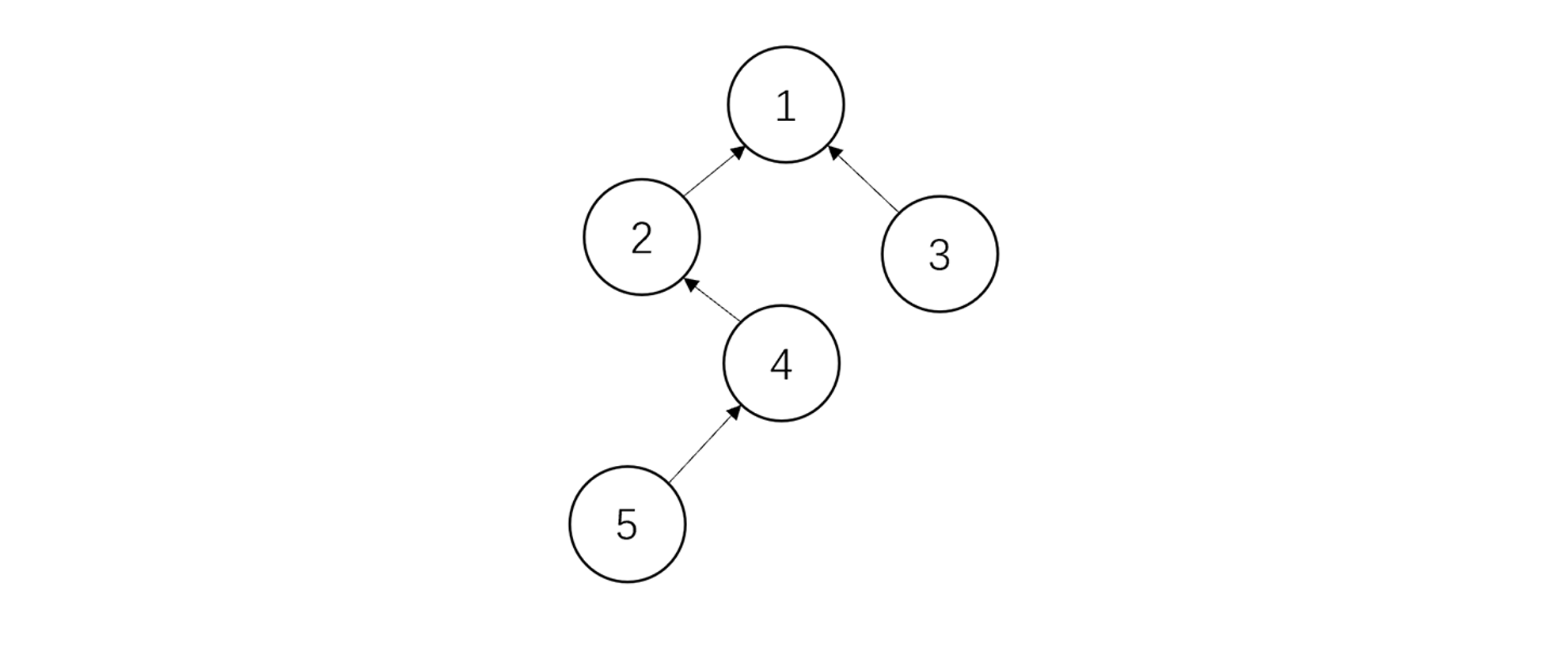

下面是节点2，将2接在其父节点的父节点上。注意，2的父节点是1，1此处没有父节点了，但我们在一开始说过，并查集的数组结构中，根节点的父节点是其本身，所以结果仍是将2接在1上，树的结构并没有改变。这也是为什么我在按秩优化中不推荐第二种写法的原因，因为在第二种写法中，S[Root]中存储的不是Root本身，而是树的高度。

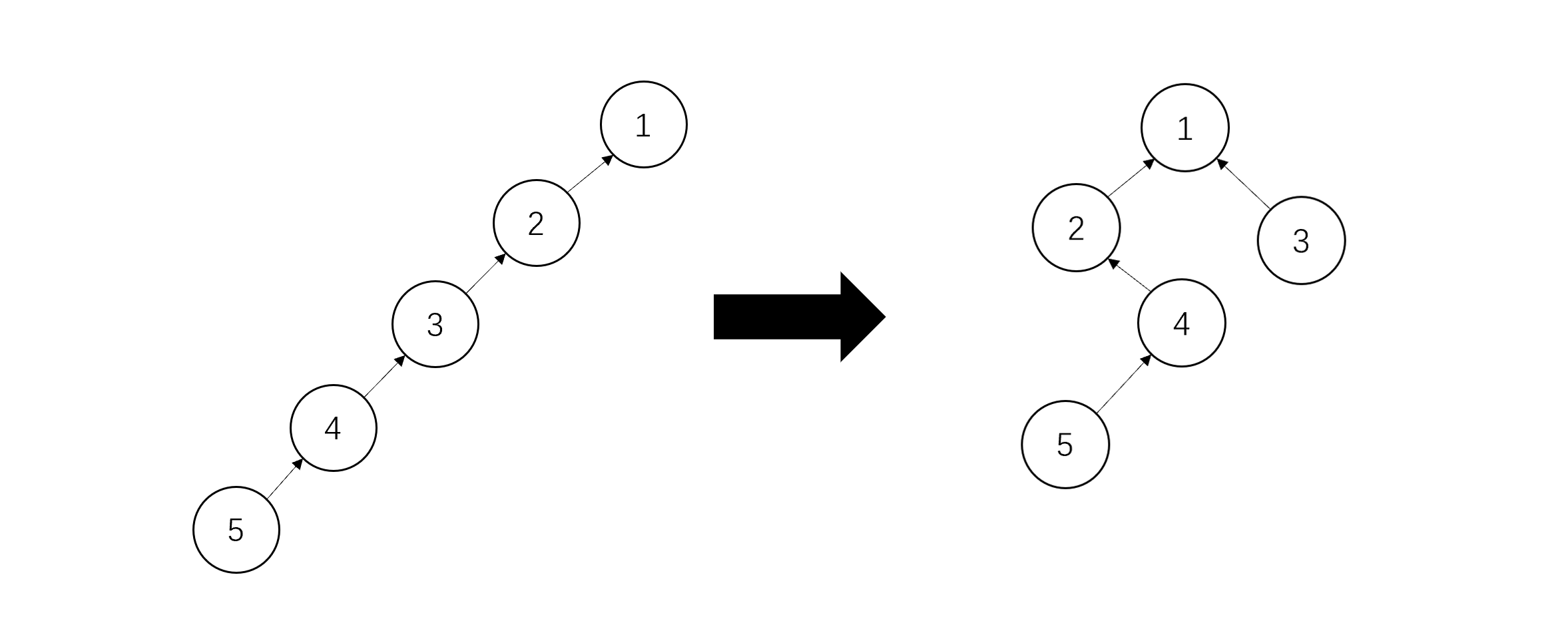
可见，经过一次路径压缩后，我们的集合树变矮了，这样若下次仍查找元素4，就可以少遍历一次。

代码实现：（其中并查集数组结构为一开始介绍的形式：根节点对应的数组元素中存储的是其本身，即S[X]=X，其中X为根节点）

SetType Find(SetType X)
{
	if (S[X] == X)
		return X;   //若是根节点，返回
	else
		return S[X] = Find(S[X]); //若不是根节点，递归寻找。同时更改树的结构
}

此外，我曾在大佬的文章中见识过一种更加简洁🐂👃的压缩路径写法：

SetType Find(SetType X)
{
	return X==S[X]?X:S[X]=Find(S[X]);
}

一行解决并查集，无话可说。

需要注意的是，若你的并查集数组采用的结构是上一部分中最后介绍的形式，即根节点对应的数组元素中存储的不是其本身，而是秩的话，需要对路径压缩代码进行些许更改：

SetType Find(SetType X)
{
	if (S[X] <= X)	//此处进行了更改。通过检验S[X]中的值是否为负来判断X是否为根节点，而非检验S[X]是否为X本身。
		return X;
	else
		return S[X] = Find(S[X]);
}

维基百科上有给出，单使用路径压缩时，时间复杂度是一个很复杂的式子，为$$Θ(n+f·(1+log_{2+f/n}n))$$
在Mark Allen Weiss的书上给出，连续M次操作最多需要$O(MlogN)$的时间。

按秩优化+路径压缩

很明显，按秩优化优化的是SetUnion函数，路径压缩优化的是Find函数，我们显然可以将两种优化合并使用（其中按秩优化为按高度合并。且并查集的结构为第一种形式。）：

SetType Find(SetType X)
{
	if (S[X] == X)
		return X;   //若是根节点，返回
	else
		return S[X] = Find(S[X]); //若不是根节点，递归寻找。同时更改树的结构
}

void SetUnion(SetType X, SetType Y)
{
    SetType Root1 = Find(X), Root2 = Find(Y);
    if(Root1 == Root2) return;
	if (Rank[Root2] > Rank[Root1])
		S[Root1] = Root2;
	else
	{
		if (Rank[Root1] == Rank[Root2]) //两个集合高度一致，随便挑一个将其接在另一个上
			Rank[Root1]++;
		S[Root2] = Root1;
	}
}

路径压缩和按秩序优化的兼容性

可见，若秩为树的大小，路径压缩和按秩优化是完全兼容的。因为路径压缩针对的是查询函数，而按秩优化针对的是合并函数，最重要的是两种优化方法并没有相互冲突之处，只需同时使用即可。

但是对于秩为树的高度的合并方法（即上一部分给出的），两者并不完全兼容，因为路径压缩会改变树的高度。这样就难以取计算他们的效率。

两者同时使用时，算法在最坏的情况下基本是线性的，其需要的时间为$O(α(n))$。在维基百科的解释中，$α(n)$为$A(x, x)$的阿克曼函式，就结果来讲，$α(n)$在n很大时整体仍小于5。